M-T curve using Monte Carlo

In MicroMagnetic, we can use Monte Carlo to compute the M-T curve. For the atomistic model with $z$ nearest neighbors, the relation between exchange constant and $T_c$ reads [1]

$$J=\frac{3k_B{T}_c}{ϵz}$$

where $ϵ$ is a correction factor. For 3D classical Heisenberg model $ϵ\approx 0.719$. In this example, we will assume $J=300k_B$ which gives $T_c=431K$. The full script is shown below.

using MicroMagnetic

#MicroMagnetic.set_float(Float32)

@using_gpu()

function relax_system_single(T)
    mesh = CubicMesh(; nx=30, ny=30, nz=30, pbc="xyz")
    sim = MonteCarlo(mesh; name="mc")
    init_m0(sim, (0, 0, 1))

    add_exch(sim; J=300 * k_B)
    add_dmi(sim; D=0)
    add_zeeman(sim; Hx=0, Hy=0, Hz=0)
    add_anis(sim; Ku=0, Kc=0)

    sim.T = 100000
    run_sim(sim; max_steps=10000, save_vtk_every=-1, save_m_every=-1)
    sim.T = T
    run_sim(sim; max_steps=50000, save_vtk_every=-1, save_m_every=-1)

    ms = zeros(1000)
    sim.T = T
    for i in 1:1000
        run_sim(sim; max_steps=100, save_vtk_every=-1, save_m_every=-1)
        t = MicroMagnetic.average_m(sim)
        ms[i] = sqrt(t[1]^2 + t[2]^2 + t[3]^2)
    end
    return sum(ms) / length(ms)
end

function relax_system()
    f = open("M_T.txt", "w")
    write(f, "#T(K)     m \n")
    for T in 10:20:20
        println("Running for $T ...")
        m = relax_system_single(T)
        write(f, "$T    $m \n")
    end
    return close(f)
end

Run the relax_system function.

relax_system()

Finally, we plot the M-T curve.

using DelimitedFiles
using CairoMakie

function plot_m_H()
    fig = Figure(; size=(400, 300))
    ax = Axis(fig[1, 1]; xlabel="T (K)", ylabel="m")

    data = readdlm("M_T.txt"; skipstart=1)
    sc1 = scatter!(ax, data[:, 1], data[:, 2]; markersize=10, label="M-T curve")
    sc1.color = :transparent
    sc1.strokewidth = 1
    sc1.strokecolor = :purple
    lines!(ax, data[:, 1], data[:, 2])

    axislegend()

    #save("M_T.png", fig)

    return fig
end

fig = plot_m_H();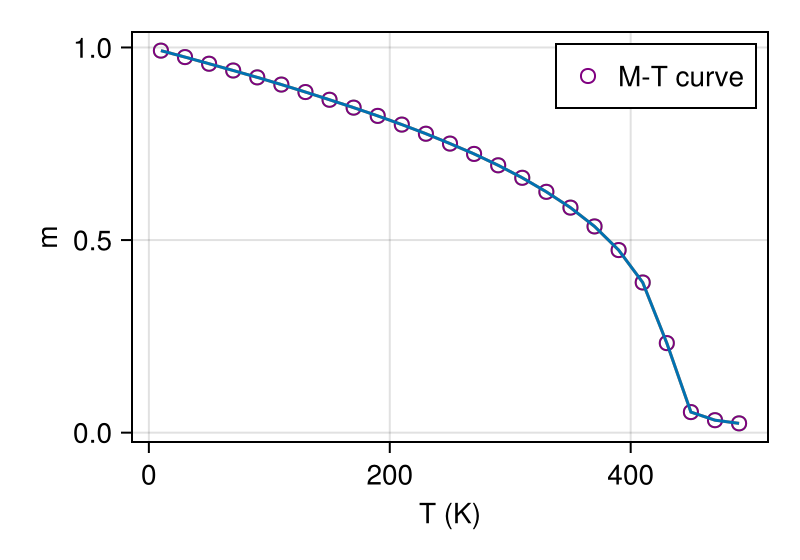

[1] Atomistic spin model simulations of magnetic nanomaterials, J. Phys.: Condens. Matter 26 (2014) 103202.