Magnetic skyrmion
In this example, we demostrate how to get a skyrmion using MicroMagnetic.jl. We use the parameters given in PRL 111 067203 (2013).
Used parameters in the simulation
| Parameter | Value |
|---|---|
| Lattice constant | |
| Spin length | |
| Magnetic moment | |
| Excahnge constant | |
| DMI | |
| External field |
We define a function to specify the problem.
julia
using MicroMagnetic
using CairoMakie
function m0_fun(i, j, k, dx, dy, dz)
r2 = (i - 25)^2 + (j - 25)^2
if r2 < 10^2
return (0.01, 0, -1)
end
return (0, 0, 1)
end
function relax_system()
mesh = CubicMesh(; nx=50, ny=50, nz=1, pbc="xy")
#We create a simulation with 'SD' driver
sim = Sim(mesh; driver="SD", name="skx")
set_mu_s(sim, mu_s_1) # set mu_s of the system
#Initialize the system using the `m0_fun` function
init_m0(sim, m0_fun)
J = 50 * k_B
add_exch(sim, J; name="exch")
add_dmi(sim, 0.5 * J; name="dmi")
Hz = 0.2 * J / mu_s_1
add_zeeman(sim, (0, 0, Hz)) # the unit of Hz is Tesla
#Relax the system
relax(sim; max_steps=2000, stopping_dmdt=0.01)
#Save the magnetization to vtk file
save_vtk(sim, "skx"; fields=["exch", "dmi"])
return sim
end
sim = relax_system();[ Info: AtomisticSim has been created.
[ Info: Bulk DMI for CubicMesh has been added!
[ Info: Static Zeeman has been added.
[ Info: Running Driver : MicroMagnetic.SD{Float64}.
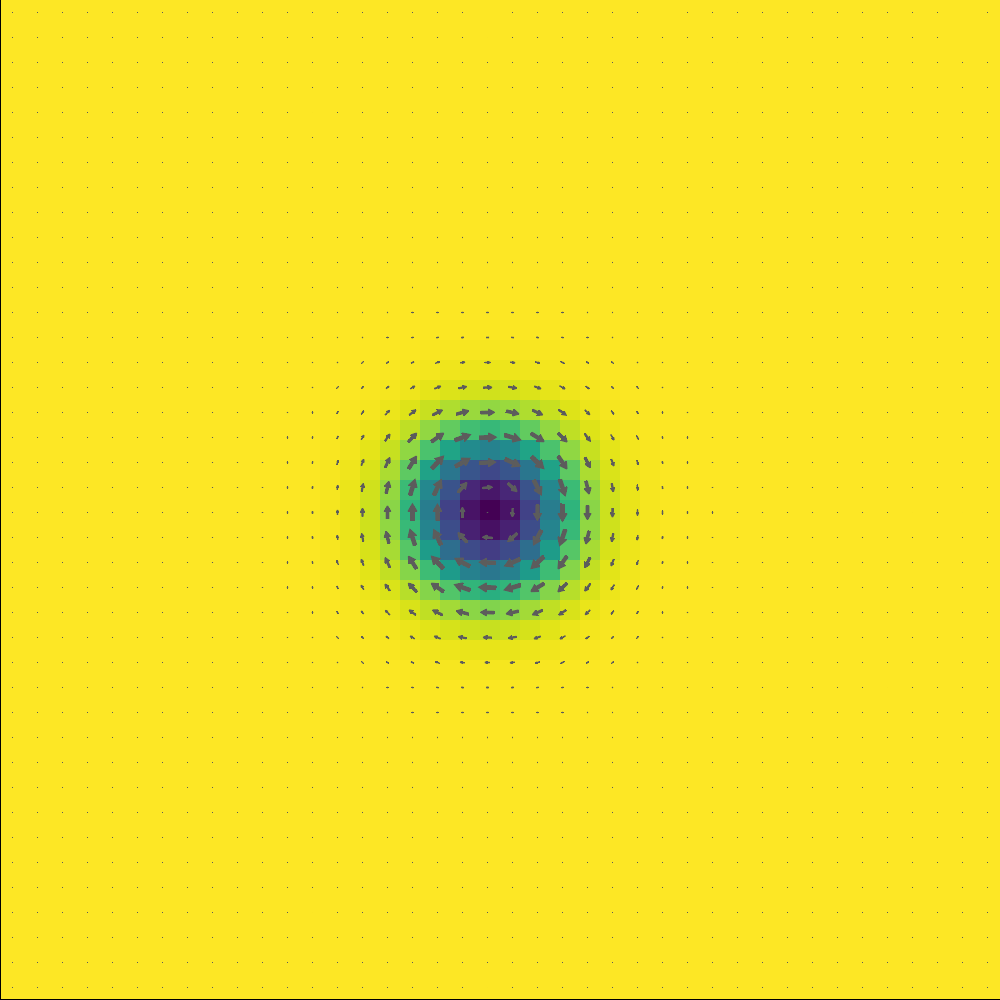
[ Info: max_dmdt is less than stopping_dmdt=0.01 @steps=39, Done!After obtain the skyrmion, we use the following script to plot the skyrmion
julia
plot_m(sim)